Алгоритмическая сложность
Алгоритмическая сложность - тема отдельного курса в классических университетских программах. Как, впрочем, и математический анализ. Однако на собеседовании Вас вряд ли попросят посчитать интеграл, а вот про сложность алгоритмов спрашивают практически всех на любую позицию программиста. А знакомо ли Вам понятие алгоритмическая сложность? А какая сложность быстрой сортировки? А это в лучшем или в худшем случае? Бывает, с горем пополам разобрались с какой-нибудь задачей на логику, но вас добивают: а какая сложность Вашего решения, можно ли ускорить? В этом посте постараюсь объяснить, что тут к чему, и не пугайтесь, если для Вас NP-полнота значит не больше, чем NP-пустота.
Важность понятия алгоритмической сложности в том, что на практике, как правило, существует разумно оптимальный способ решить задачу. Использовав его, дальнейшая оптимизация будет улучшать производительность на 10-50%, что потребует ещё в два или пять раз больше времени на разработку. Одновременно с этим, неправильно выбранный способ решения будет работать медленнее в десять, в сто, в тысячу раз. На практике система виснет на простых операциях, загрузка занимает секунды, а всевозможные запланированные задачи запускаются по ночам и работают часами. И объёмы данных отнюдь не терабайты, достаточно нескольких миллионов записей. И я расскажу, почему.
Сложность алгоритма - это ответ на вопрос сколько действий придётся совершить, чтобы решить задачу, в зависимости от параметров задачи. Разнородных параметров в задаче может быть много, и разнородных действий тоже. И то и другое нужно сократить до одного: один параметр и одно действие, остальное отбросить. Например, Вы листаете договор из тысячи страниц и подписываете каждую. Входной параметр такой задачи будет количество страниц, а действие - поставить подпись. Перелистывание страниц мы не считаем за важное действие, потому что это намного быстрее подписи. Не важно, сколько времени уйдёт на всё, два часа или два дня - кто-то расписывается быстрее, кто-то медленнее. Но каждому потребуется 1000 действий для выполнения алгоритма. Если обобщить, то требуется N действий при N страницах. Легко можно посчитать, что если Вы подписали договор из 10 страницы за 10 минут, то на 60 страниц Вы потратите час. Если оптимизировать процесс и подписывать только первую страницу, то потребуется одна минута вне зависимости от количества страниц.
Другой пример - на бумаге разлинован квадрат со стороной 10. В каждой клетке нужно поставить точку, всего точек 100 (N^2). Если потребовалось 10 минут на всё про всё, то, чтобы повторить алгоритм на квадрате со стороной 60, потребуется 10 / 100 * 60 * 60 = 360 минут, то есть 6 часов. Итого в одной задаче увеличив входной параметр в шесть раз, мы потратили в 6 раз больше времени, а в другой - в 36. Разница колоссальная.
Я привёл три примера сложности алгоритма: константную, порядка N и порядка N^2. У программистов принято говорить "О большое от". Ниже для порядка я приведу строгое определение, но на практике требуется лишь указать порядок скорости роста времени работы алгоритма при росте основного параметра задачи. Коэффициент перед функцией от N не важен: если требуется N^2 действие или 100 * N^2 действий - это всё равно будет O(N^2), потому что в обоих случаях рост N в два раза увеличивает время работы в четыре.
"O"-обозначение используется, если нужно определить асимптотическую верхнюю границу для функции f(n),
равную времени работы алгоритма в зависимости от основного параметра задачи.
Определение взято из книги Томаса Кормена "Алгоритмы. Построение и анализ.".
Для данной функции g(n) обозначение O(g(n)) означает множество функций
O(g(n)) = {f(n): существуют положительные константы c и n0,
такие что 0<=f(n)<=cg(n) для всех n>=n0}
Программисты не следуют педантично строгому определению и упрощают до примерно такого: f(n) = O(g(n)), если функция f(n) при больших n ведёт себя пропорционально функции g(n).
На практике чаще всего встречаются пять функций определяющих сложность алгоритма:
- O(1)
- Константа. Время работы фиксировано и не зависит от размера задачи.
- O(log(n))
- Логарифм. Основание логарифма опускается, потому что переход от одного основания к другому это умножение на константу.
- O(n)
- Линейная сложность. Время растёт пропорционально размеру задачи.
- O(n*log(n))
- Сложность, которая называется "Эн лог эн". Все хорошие алгоритмы сортировки имеют такую сложность.
- O(n*n)
- Квадратичная сложность. Например, всевозможные попарные операции в массивах.
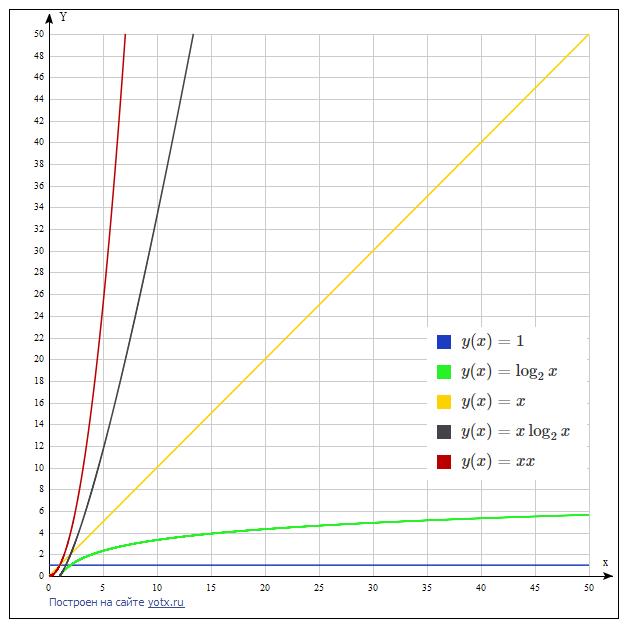
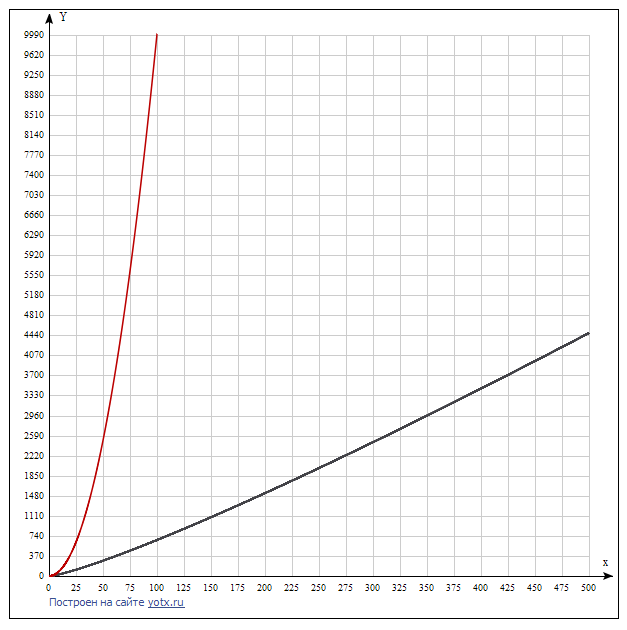
На графике ниже показана скорость роста этих функций в сравнении. Видно, что каждая следующая функция растёт намного быстрее предыдущей. Поэтому следует искать алгоритм, решающий задачу с наименьшей сложностью. Как правило, такой алгоритм сложнее и не всегда очевиден. На втором графике сравниваются две последние функции, чтобы показать, что между ними тоже существенное различие.
Java разработчику желательно знать несколько основных алгоритмов, понимать их сложность и область применения. Они собраны в таблице ниже.
| Алгоритм | Лучший случай | Средний случай | Худший случай | Комментарий |
|---|---|---|---|---|
| Получение элемента по индексу в массиве или ArrayList | O(1) | O(1) | O(1) | Область памяти, выделенная под массив, непрерывна, а размер элемента фиксирован. |
| Добавление элемента в конец ArrayList / LinkedList, в начало LinkedList | O(1) | O(1) | O(1) для LinkedList, O(n) для ArrayList | Для ArrayList требуется небольшое уточнение: периодически приходится расширять массив, когда он переполняется, и эта операция формально стоит O(n), хотя и используется очень эффективная функция System.arraycopy. Но так как расширение производится в полтора раза (int newCapacity = oldCapacity + (oldCapacity >> 1);), то общее количество таких расширений - логарифм, то есть пренебрежимо мало по сравнению с O(n), поэтому в среднем сложность O(1). |
| Добавление в середину, удаление из ArrayList | O(n) | O(n) | O(n) | Требуется скопировать все элементы списка справа от добавляемого или удаляемого элемента. Формально эта операция требует O(n), но, как и при расширении массива, элементы не копируются по одному, а применяется операция System.arraycopy. Также может потребоваться расширить массив, как и при добавлении в конец, но на суммарную сложность это не влияет. |
| Добавление в середину, удаление из LinkedList | O(1) | O(1) | O(1) | Такая производительность достигается только если уже есть ссылка на элемент (Iterator, ListIterator). Иначе нужно сначала найти элемент по индексу, что стоит O(n) |
| Операции по ключу в HashMap | O(1) | O(1) | O(n) | Худший случай имеет место скорее при плохой реализации hashCode, а не из-за специфичных входных данных. При хорошей функции hashCode достигается лишь в теории. Если углубиться в реализацию HashMap в Java, то следует отметить, что начиная с версии 1.8, элементы внутри одной корзины (bucket) хранятся в сбалансированном дереве. Это позволяет в худшем случае добиться сложности O(log(n)) при условии, что хэш коды элементов различны. В противном случае HashMap вырождается в связанный список и сложность в худшем случае будет O(n). |
| Операции по ключу в TreeMap | O(1) | O(log(n)) | O(log(n)) | TreeMap реализован на основе красно-чёрного дерева. Лучший случай - если нашли элемент сразу на вершине дерева. Скорее теоретический случай, чем практический. |
| Бинарный поиск | O(1) | O(log(n)) | O(log(n)) | Бинарный поиск по сути аналогичен поиску в сбалансированном бинарном дереве. |
| Поиск в неотсортированном списке или массиве, ArrayList, LinkedList | O(1) | O(n) | O(n) | Нужно перебрать все элементы по очереди. |
| Сортировка слиянием | O(nlog(n)) | O(nlog(n)) | O(nlog(n)) | Также алгоритм требует O(n) дополнительной памяти. В OpenJDK используется TimSort - "гибридный алгоритм сортировки, сочетающий сортировку вставками и сортировку слиянием". TimSort быстрее на частично отсортированных данных. |
| Быстрая сортировка, она же QuickSort | O(nlog(n)) | O(nlog(n)) | O(n^2) | Не требует дополнительной памяти, кроме O(log n) для стека рекурсивных вызовов. |
| Медленные алгоритмы сортировки: пузырьковая, вставками | O(n^2) | O(n^2) | O(n^2) | Медленные алгоритмы сортировки используются, в частности, на коротких массивах. Например, в реализации TimSort в OpenJDK если количество элементов меньше 32, то используется сортировка вставками, а если больше - то сортировка слиянием. |
Несколько слов об алгоритме быстрой сортировки (QuickSort). Сам алгоритм хорошо описан здесь. Алгоритм имеет пару нюансов понимания и реализации, без которых его производительность может падать до O(n^2), и алгоритм становится интересен лишь в академических целях, но не в практических.
- В качестве опорного элемента должен выбираться случайный элемент. Левый, правый или средний - не подходят. Тогда в среднем длина большей части массива будет в три раза больше меньшей (соотношение три к одному). То есть хуже, чем разбиение точно пополам, но длина цепочки рекурсивных вызовов всё равно будет логарифмом. Вероятность на каждой итерации случайно попадать в максимальный или минимальный элемент пренебрежимо мала (примерно 0.001^1000 для массива из тысячи элементов). В таком случае даже худшее время работы тоже будет O(nlog(n)), а не O(n^2), как принято говорить. Хотя это сугубо моё мнение, обычно говорят, что теоретически может быть квадратичная сложность, но на практике совсем редко.
- Следует выбирать версию алгоритма, которая делит подмассив на три части: меньшие опорного, равные ему, и большие. Классическое определение алгоритма разбивает на две части: меньшие либо равные и большие, но при этом делается предположение, что все элементы различны. Если пренебречь этой деталью и применить классическую реализацию к массиву равных элементов, то получим сложность O(n^2). То есть дольше всего алгоритм работает когда и делать-то ничего не нужно! Если выделить элементы, равные опорному в отдельную группу, то для массивов с повторяющимися элементами наоборот получим существенный выигрыш.
В реальных приложениях с качеством кода ниже среднего можно встретить неэффективную реализацию типовых задач. Например, пересечение двух коллекций можно посчитать за O(n), скопировав данные в HashSet, а на деле используется полный попарный перебор за O(n^2). Или же мы ищем данные в списке много раз за O(n), хотя можно отсортировать его один раз или же использовать TreeSet и тогда воспользоваться бинарным поиском за O(log(n)).
Разберу одну задачу из типовых вопросов с собеседований. Постановка задачи такова: удалить из списка элементы с нечётными номерами, то есть каждый второй элемент. На stackoverflow есть страница с похожим вопросом, хоть и старая и с небольшим количеством комментариев. Но ответы, которые предлагаются в качестве решений довольно показательны. Код на GitHub.
К сожалению, в вопросе изначально уточняется, что удалить нужно из ArrayList ("Remove odd elements from ArrayList while iterating"). Мы знаем, что удаление элемента из ArrayList приведёт к копированию всей хвостовой части, то есть будет стоить O(n), поэтому суммарная сложность будет O(n^2). Разумно же ожидать, что удаление будет произведено за один проход по списку, то есть O(n), и это легко достигается для LinkedList. Поэтому изначально использование ArrayList для такого сценария неверно. Если мы завязаны на ArrayList, то в реальном приложении стоит сделать копию массива и потом обновить ссылку. Если и это не применимо, то можно написать сложный код, который будет копировать элементы на пустые места, а потом удалит хвост, но всё-таки завершится за один проход по массиву.
Работать со списком по индексам элементов неестественно. Обычно предикат будет зависеть от самих элементов списка, и тогда решение было бы таким:
//java8
elements.removeIf(s -> Long.parseLong(s) % 2 == 1); //before java8
for (Iterator<String> iterator = elements.iterator(); iterator.hasNext(); ) {
String next = iterator.next();
if(Long.parseLong(next) % 2 == 1) {
iterator.remove();
}
}
Но на собеседованиях часто даются такие задачи с небольшим подвохом, чтобы проверить понимание нюансов.
Решения исходной задачи:
//java8
AtomicInteger counter = new AtomicInteger(0);
elements.removeIf(s -> counter.incrementAndGet() % 2 == 0); //before java8
int counter = 0;
for (Iterator<String> iterator = elements.iterator(); iterator.hasNext(); ) {
iterator.next();
if (counter++ % 2 == 1) {
iterator.remove();
}
} //before java8
//хитрый способ избежать введения переменной counter. Следует избегать таких неочевидных приёмов.
for (ListIterator<String> literator = elements.listIterator(elements.size()); literator.hasPrevious();) {
literator.previous();
if (literator.previousIndex() % 2 == 0) {
literator.remove();
}
} //O(n) for ArrayList
//решение на крайний случай, если вероятны проблемы с производительностью, но от ArrayList не уйти.
//объём кода не соответствует сложности задачи, читаемость его тоже низкая, придётся объяснять в комментариях,
//почему так, а не иначе
//если применить это решение к LinkedList, то получим O(n^2)
removeFromArrayList(elements, i -> i % 2 == 1);
static void removeFromArrayList(ArrayList<String> elements, IntPredicate removeIf) {
int lastIndex = 0;
for (int i = 0; i < elements.size(); i++) {
if (!removeIf.test(i)) {
elements.set(lastIndex, elements.get(i));
lastIndex++;
}
}
int extraElementsCount = elements.size() - lastIndex;
//unfortunately, we can't use protected removeRange method
for (int i = 0; i < extraElementsCount; i++) {
elements.remove(elements.size() - 1);
}
}
Прокомментирую решения, предложенные на stackoverflow.
//1.
//Корректное решение. O(n^2) для ArrayList, O(n) для LinkedList
int i = 0;
for (Iterator<String> it = words.iterator(); it.hasNext(); ) {
it.next(); // Add this line in your code
if (i % 2 != 0) {
it.remove();
}
i++;
} //2.
//Некорректное решение. O(n^2) для ArrayList, O(n^2) для LinkedList.
//Ошибочный результат при дублирующихся значениях в списке.
int i = 0;
List<String> list = new ArrayList<String>();
for (String word:words) {
if (i % 2 != 0) {
//it.remove();
list.add(word);
}
i++;
}
words.removeAll(list); //элементы удаляются по значению!
//додумать решение можно так (ещё заменить условие на ==0):
//words.clear();
//words.addAll(list); //3.
//На этом примере я потерпел фиаско. Я был уверен, что код не работает, потому что размер и индексы будут изменяться по ходу работы алгоритма,
//что, удаляя элемент с индексом 2, мы удаляем элемент с индексом 3 в исходном массиве. Всё перепуталось и не может дать верный результат...
//Но! результат верный. На каждом шагу мы удаляем элемент, сдвигаем все индексы на 1 влево, но увеличиваем счётчик на 1, а не на 2.
//здесь мои полномочия всё, как говорится
//Сложность O(n^2) для ArrayList и LinkedList
int i = 1;
while (i < words.size()) {
words.remove(i++);
} //4.
//Корректное решение. Единственное из предложенных O(n) для ArrayList; O(n^2) для LinkedList.
//Минус - тяжело читаемый код. Два счётчика, называются i, j. Причём j всегда равно i/2.
//Если это писали не Вы, то придётся запускать отладку, чтобы разобраться.
int j = 0;
for(int i = 0 ; i < integers.size(); i++){
if( i % 2 == 0){
integers.set(j, integers.get(i));
j++;
}
}
int half = integers.size()%2==0 ? integers.size()/2 : integers.size()/2 + 1;
integers.subList(half , integers.size()).clear();//буду знать, что subList не создаёт новый список, а лишь ссылку на подсписок текущего.
//поэтому хвост можно обрезать вот так в одну строчку.
Пример с удалением один из самых базовых и простых. Подобным образом можно мусолить любые коллекции и операции с ними: LinkedList, ArrayList, HashMap, TreeMap, LinkedHashMap, CopyOnWriteArrayList и так далее. В данном посте я этого делать не буду, перейду к итогу всего что я тут понаписал.
Заключение
Приходится соблюдать тонкий баланс между оптимальностью решения по производительности, читаемостью и лаконичностью кода и здравым смыслом. Главное понимать насколько быстро можно решить типовую задачу и подобрать правильные структуры данных и операции с ними. На интервью на позицию Java разработчика часто вопрос по данной тематике будет вторым (после "методов класса Object" или "расскажите о последнем проекте").